8.7

A small lawnmower company produced 1,500 lawnmowers in 1998. In an effort to determine how maintenance-free these units were, the company decided to conduct a multiyear study of the 1998 lawnmowers. A sample of 200 owners of these lawnmowers was drawn randomly from company records and contacted. The owners were given an 800 number and asked to call the company when the first major repair was required for the lawnmowers. Owners who no longer used the lawnmower to cut their grass were disqualified. After many years, 187 of the owners had reported. The other 13 disqualified themselves. The average number of years until the first major repair was 5.3 for the 187 owners reporting. It is believed that the population standard deviation was 1.28 years. If the company wants to advertise an average number of years of repair-free lawn mowing for this lawnmower, what is the point estimate? Construct a 95% confidence interval for the average number of years until the first major repair.

 

N = 1500

n = 200 187

 = 5.3

µ = ?

= 1.28 years

 

Sample size 187 > 5% of the population (1500), therefore we will use the Finite Correction Factor formula.

 

 

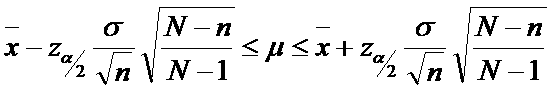
The z value for a 95% confidence interval is 1.96, i.e. (0.95/2 = 0.4750), using Table A.5 translates 0.4750 to a z value of 1.96.

 

The point estimate  is 5.3.

 

 

 

 

 

 

 

 

 

 

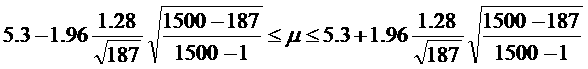
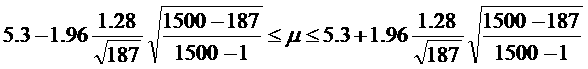
With 95% confidence, we estimate that the population mean is between 5.13 and 5.37.